Hdu2084 数塔

发表于 | 更新于: | 分类于 ， | | 阅读数
字数统计: 503 | 阅读时长 ≈ 2

Description

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

DP

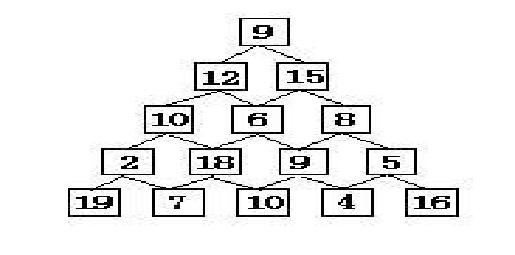
已经告诉你了，这是个DP的题目，你能AC吗?

Input

输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

Output

对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。

Sample Input

1
2
3
4
5
6
7
1
5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

Sample Output

1
30

Analysis

DP的裸题，思路是每个结点都存储走到当前结点经过的结点的数字所能组成的最大和，在最低层扫一遍进行比较，有些贪心的味道。处理好最左侧与最右侧的递推关系，中间的的递推式为

1
dp[i][j] = to[i][j] + max(dp[i - 1][j - 1], dp[i - 1][j]);

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int to[101][101];
int dp[101][101];
int main()
{
	int C;
	cin >> C;
	while (C-- != 0)
	{
		int N;
		cin >> N;
		memset(to, 0, sizeof(to));
		for (int i = 1; i <= N; i++)
		{
			for (int j = 1; j <= i; j++)
			{
				cin >> to[i][j];
			}
		}
		memset(dp, 0, sizeof(dp));
		dp[1][1] = to[1][1];
		for (int i = 2; i <= N; i++)
		{
			dp[i][1] = to[i][1] + dp[i - 1][1];
			dp[i][i] = to[i][i] + dp[i - 1][i - 1];
		}
		for (int i = 3; i <= N; i++)
		{
			for (int j = 2; j <= i - 1; j++)
			{
				dp[i][j] = to[i][j] + max(dp[i - 1][j - 1], dp[i - 1][j]);
			}
		}
		int maxs = 0;
		for (int j = 1; j <= N; j++)
		{
			if (dp[N][j] > maxs)
			{
				maxs = dp[N][j];
			}
		}
		cout << maxs << endl;
	}
	return 0;
}