Poj3253 Fence Repair

发表于 | 更新于: | 分类于 ， | | 阅读数
字数统计: 960 | 阅读时长 ≈ 4

Description

Farmer John wants to repair a small length of the fence around the pasture. He measures the fence and finds that he needs N (1 ≤ N ≤ 20,000) planks of wood, each having some integer length Li (1 ≤ Li ≤ 50,000) units. He then purchases a single long board just long enough to saw into the N planks (i.e., whose length is the sum of the lengths Li). FJ is ignoring the “kerf”, the extra length lost to sawdust when a sawcut is made; you should ignore it, too.FJ sadly realizes that he doesn’t own a saw with which to cut the wood, so he mosies over to Farmer Don’s Farm with this long board and politely asks if he may borrow a saw.Farmer Don, a closet capitalist, doesn’t lend FJ a saw but instead offers to charge Farmer John for each of the N-1 cuts in the plank. The charge to cut a piece of wood is exactly equal to its length. Cutting a plank of length 21 costs 21 cents.Farmer Don then lets Farmer John decide the order and locations to cut the plank. Help Farmer John determine the minimum amount of money he can spend to create the N planks. FJ knows that he can cut the board in various different orders which will result in different charges since the resulting intermediate planks are of different lengths.

Input

Line 1: One integer N, the number of planks Lines 2..N+1: Each line contains a single integer describing the length of a needed plank

Output

Line 1: One integer: the minimum amount of money he must spend to make N-1 cuts

Sample Input

1
2
3
4
3
8
5
8

Sample Output

1
34

Analysis

（以下方法来自《挑战程序设计竞赛.第2版》）

题目貌似很难入手，但是可以用略微奇特的贪心法来求解。

首先，切割的方法可以用如下二叉树来描述：

二叉树

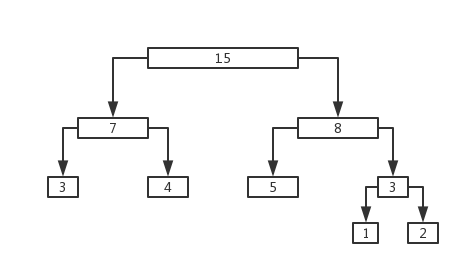
每一个叶子节点对应了切割出的一块块木板。叶子节点的深度（第一个节点为0）就对应了为了得到对应木板所需的切割次数，开销的合计就是各叶子节点的

​ 木板的长度 X 节点的深度

的总和。例如，上图示例的全部开销就可以这样计算：

​ 3 X 2 + 4 X 2 + 5 X 2 + 1 X 3 + 2 X 3=33

于是，此时的最佳切割方法首先应该具有如下性质：

​ 最短的板与次短的板的节点应当是兄弟节点

对于最优解来讲，最短的板应当是深度最大的叶子节点之一。所以与这个叶子节点同一深度的兄弟节点一定存在，并且由于同样是最深的叶子节点，所以应该对应于次短的板。

不妨将Li按照大小顺序排列，那么最短的板就应该是L1而次短的则是L2。如果它们在二叉树中是兄弟节点，就意味着它们是从一块长度为(L1+L2)的板切割而来的。由于切割顺序是自由的，不妨当作是最后被切割。这样一来，在这次切割前就有

​ (L1+L2),L3,L4,…,LN

这样的N-1块木板存在。与以上讨论的方式相同，递归地将这N-1块木板的问题求解，就可以求出整个问题的答案。这样实现的话，虽然复杂度是O(N^2)，对于题目的输入规模来说，已经足以在时间限制内通过了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int n, l[20005];
int main()
{
	while (cin >> n)
	{
		for (int i = 0; i < n; i++)
		{
			cin >> l[i];
		}
		ll ans = 0;
		//直到计算到木块为1块时停止
		while (n > 1)
		{
			//求出最短的板mii1和次短的板mii2
			int mii1 = 0, mii2 = 1;
			if (l[mii1] > l[mii2])
				swap(mii1, mii2);
			for (int i = 2; i < n; i++)
			{
				if (l[i] < l[mii1])
				{
					mii2 = mii1;
					mii1 = i;
				}
				else if (l[i] < l[mii2])
				{
					mii2 = i;
				}
			}
			//将两块板拼合
			int t = l[mii1] + l[mii2];
			ans += t;
			//如果最短板mii1是n-1，因为n要减少，所以需要把它提前，防止下次循环时数据已经被丢弃
			if (mii1 == n - 1)
				swap(mii1, mii2);
			l[mii1] = t;
			l[mii2] = l[n - 1];
			n--;
		}
		cout << ans << endl;
	}
	return 0;
}