Poj1328 Radar Installation

发表于 | 更新于: | 分类于 ， | | 阅读数
字数统计: 728 | 阅读时长 ≈ 4

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d. We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

图片

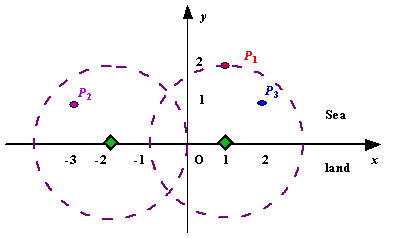
​ Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases. The input is terminated by a line containing pair of zeros

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. “-1” installation means no solution for that case.

Sample Input

1
2
3
4
5
6
7
8
9
3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

1
2
Case 1: 2
Case 2: 1

Analysis

在直线上放置点，使直线上方的所有点都位于直线上点半径d范围内，求最少放置多少个点。

可以换一种方法思考，如果上方的点在直线上点的d范围内，那么直线上点也一定在上方点d范围内，那么以上方点为圆心，d为半径作圆，与直线相交得到一条弦，直线上点必须放置在这条弦的区间范围内，这样就可以采用贪心思想，从左往右将有重叠部分的区间合并，直到无法再合并时，放置的点数再加一，最后得到最少解。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
int n;
double d;
struct p
{
	double x, y;
};
p point[1005];
p que[1005];
bool operator < (p a, p b)
{
	return a.x < b.x;
}
int main()
{
	int Case = 1;
	while (cin >> n >> d)
	{
		memset(point, 0, sizeof(point));
		memset(que, -10000, sizeof(que));
		if (n == 0)
			break;
		bool flag = 1;
		int count = 0;
		int ans = 1;
		for (int i = 0; i < n; i++)
		{
			cin >> point[i].x >> point[i].y;
			if (point[i].y > d)
				flag = 0;
		}
		sort(point, point + n);
		for (int i = 0; i < n; i++)
		{
			double dx = sqrt(d*d - point[i].y*point[i].y);
			que[i].x = point[i].x - dx;
			que[i].y = point[i].x + dx;
		}
		for (int i = 1; i < n ; i++)
		{
			if (que[i - 1].y < que[i].x)
			{
				ans++;
			}
			else if (que[i - 1].y >= que[i].x&&que[i - 1].y <= que[i].y)
			{
				que[i].y = que[i - 1].y;
			}
			else if (que[i - 1].x > que[i].x&&que[i - 1].y < que[i].y)
			{
				que[i].x = que[i - 1].x;
				que[i].y = que[i - 1].y;
			}
		}
		if (flag == 0 || d <= 0)
		{
			ans = -1;
		}
		cout << "Case " << Case << ": " << ans << endl;
		Case++;
	}
	return 0;
}