2.1 文法的直观概念
语言是由句子组成的集合,是一组记号所构成的集合。
语言研究的三个方面:语法(Syntax):表示构成语言句子的各个记号之间的组合规律;语义(Semantics):表示按照各种表示方法所表示的各个记号的特定含义。(各个记号和记号所表示的对象之间的关系);语用(Pragmatics)表示在各个记号所出现的行为中,它们的来源、使用和影响。
如果不考虑语义和语用,只从语法这一侧面来看语言,这种意义下的语言称作形式语言。
形式语言抽象地定义为一个数学系统。
“形式”是指:语言的所有规则只以什么符号串能出现的方式来陈述。
形式语言理论是对符号串集合的表示法、结构及其特性的研究。是程序设计语言语法分析研究的基础。
文法:描述词法、语法规则的工具。用一组规则严格定义句子的结构,即对含有“无穷句子”的语言进行“有穷的表示”。
2.2 符号和符号串
字母表$\Sigma$:元素的非空有穷集合。(又称为符号集)
符号:字母表中的元素。例如,汉语的字母表:包括汉字、数字及标点符号等;英文的字母表:${a,b,… z ,A,B,… ,Z}$;二进制的字母表:${0,1}$;标识符的字母表: ${a … z ,A … Z , 0 … 9 , _ }$。
符号串:由字母表$\Sigma$中的符号组成的任何有穷序列。空符号串$\epsilon$(没有符号的符号串)是$\Sigma$上的符号串。符号串不仅表示由哪些符号组成,还表示符号的顺序。
符号串的长度:符号串$x$中符号的个数,用$|x|$表示。
头、尾、固有头、固有尾:
$z=xy$中
$x$是$z$的头;$y$是$z$的尾
若$y$非空,$x$是$z$的固有头;若$x$非空,$y$是$z$的固有尾。
符号串的连接:$x,y$的连接即$xy$(把$y$的符号写在$x$符号后面)。
符号串的方幂:对符号串$x$,把它自身连接$n$次得到符号串$z,z=xxx…x,$记作:$z=x^n,x^0=\epsilon,x^1=x,x^2=xx,……$
符号串集合:集合A中的一切元素都是某字母表上的符号串,则称A为该字母表上的符号串集合。
符号串集合的乘积:$AB={xy|x\in A且y\in B}$。
集合的闭包:指定字母表$V$之后,可用$V^$表示$V$上所有有穷长度的串的集合。$V^+$为$V$的正闭包*。
$V^*=V^0\cup V^1\cup…\cup V^n,V^+=V^1\cup…\cup V^n$
2.3 文法和语言的形式定义
规则(重写规则、产生式、生成式),是形如$\alpha\rightarrow\beta或\alpha::=\beta$的$(\alpha,\beta)$有序对,其中$\alpha\in V^+,\beta\in V^*,\alpha$称为规则的左部,$\beta$称为规则的右部。
定义2.1 文法$G$定义为四元组$(V_N,V_T,P,S)$。$V_N$为非终结符集,$V_T$为终结符集,$P$为产生式集合(规则集合),$S$为开始符号(识别符号)。其中$V_N、V_T、P$是非空有穷集,$S\in V_N$,并且$S$至少在一条规则中作为左部出现,$V_N\cap V_T=\empty$,$V=V_N\cup V_T,V$称为文法$G$的字母表(字汇表)。
定义2.2 设$\alpha\rightarrow\beta$是文法$G=(V_N,V_T,P,S)$的规则(或说是P中的一个产生式),$\gamma$和$\delta$是$V^*$中的任意符号,若有符号串$v、w$满足
则说$v$(应用规则$\alpha\rightarrow\beta$)直接产生$w$,或说$w$是$v$的直接推导,或说$w$直接归约到$v$,记作$v\Rightarrow w$。
定义2.3 如果存在直接推导的序列
则称$v$推导出(产生)$w$(推导长度为$n$),或称$w$归约到$v$,记作$v\Rightarrow^+w$。
定义2.4 若有$v\Rightarrow^+w$,或$v=w$,则记作$v\Rightarrow^*w$。
定义2.5 设$G[S]$是一个文法,如果符号串$x$是从识别符号推导出来的,即有$S\Rightarrow^x$,则称$x$是文法$G[S]$的句型。若$x$仅由终结符号组成,即$S\Rightarrow^x,x\in V_T^*$,则称$x$为$G[S]$的句子。
定义2.6 文法$G$所产生的语言定义为集合${x|S\Rightarrow^x,其中S为文法识别符号,且x\in V_T^}$。可用$L(G)$表示该集合。
若$L(G_1)=L(G_2)$,则称文法$G_1$和$G_2$是等价的,即两个不同的文法能够产生相同的语言。
2.4 文法的类型
设$G=(V_N,V_T,P,S)$为一个文法,有
0型文法(PSG):若$P$中的每一个产生式$\alpha\rightarrow\beta$是这样一种结构:$\alpha\in(V_N\cup V_T)^$且至少含有一个非终结符,而$\beta\in(V_N\cup V_T)^$,则$G$是一个0型文法。
1型文法(CSG):若$P$中的每一个产生式$\alpha\rightarrow\beta$均满足$|\beta|\geq|\alpha|$,仅仅$S\rightarrow\epsilon$除外,则文法$G$是1型或上下文有关的(context-sensitive)。
2型文法(CFG):若$P$中的每一个产生式$\alpha\rightarrow\beta$满足:$\alpha$是一个非终结符,$\beta\in(V_N\cup V_T)^*$,则此文法称为2型的或上下文无关的(context-free)。
3型文法(RG):若P中的每一个产生式的形式都是$A\rightarrow aB$或$A\rightarrow a$,其中$A$和$B$都是非终结符,$\alpha\in V_T^*$,则$G$是3型文法或正规文法。
2.5 上下文无关文法及其语法树
给定文法$G=(V_N,V_T,P,S)$,对于$G$的任何句型都能构造与之关联的语法树(推导树)。这棵树满足下列4个条件:
(1)每个结点都有一个标记,此标记是$V$的一个符号。
(2)根的标记是$S$。
(3)若一个结点$n$至少有一个它自己除外的子孙,并且有标记$A$,则$A$肯定在$V_N$中。
(4)如果结点$n$的直接子孙从左到右的次序是结点$n_1,n_2,\cdots,n_k$,其标记分别为$A_1,A_2,\cdots,A_k$,那么$A\rightarrow A_1A_2\cdots A_k$一定是$P$中的一个产生式。
如果在推导的任何一步$\alpha\Rightarrow\beta$,其中$\alpha、\beta$是句型,都是对$\alpha$中的最左(最右)非终结符进行替换,则称这种推导为最左(最右)推导。在形式语言中,最右推导被称为规范推导,由规范推导所得的句型称为规范句型。
若一个文法存在某个句子对应两棵不同的语法树,则称这个文法是二义的。或者,若一个文法存在某个句子有两个不同的最左(右)推导,则称这个文法是二义的。产生某上下文无关语言的每一个文法都是二义的,则称此语言是先天二义的。注:程序设计语言的文法不要二义。
2.6 句型的分析
句型分析就是识别一个符号串是否为某文法的句型,是某个推导的构造过程。在语言的编译实现中,把完成句型分析的程序称为分析程序或识别程序。
分析算法又称识别算法。从左到右的分析算法即总是从左到右地识别输入符号串。首先识别符号串中的最左符号,进而依次识别右边的一个符号
分析算法分为自顶向下和自底向上,前者从文法的开始符号出发,反复使用各种产生式,寻找与输入符号匹配的推导;后者从输入符号串开始,逐步进行归约,直至归约到文法的开始符号。两种方法反映了两种不同的语法树的构造过程。
2.6.1 自顶向下的分析方法
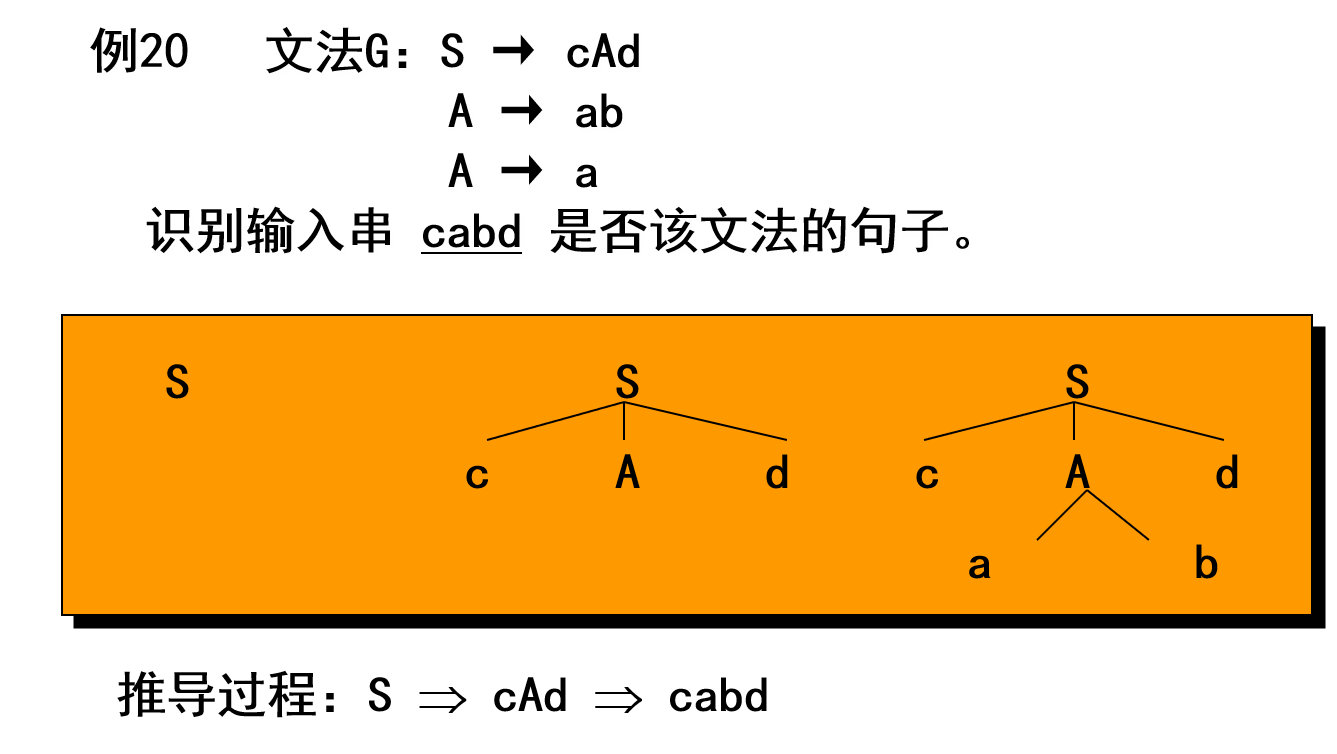
2.6.2 自底向上的分析方法
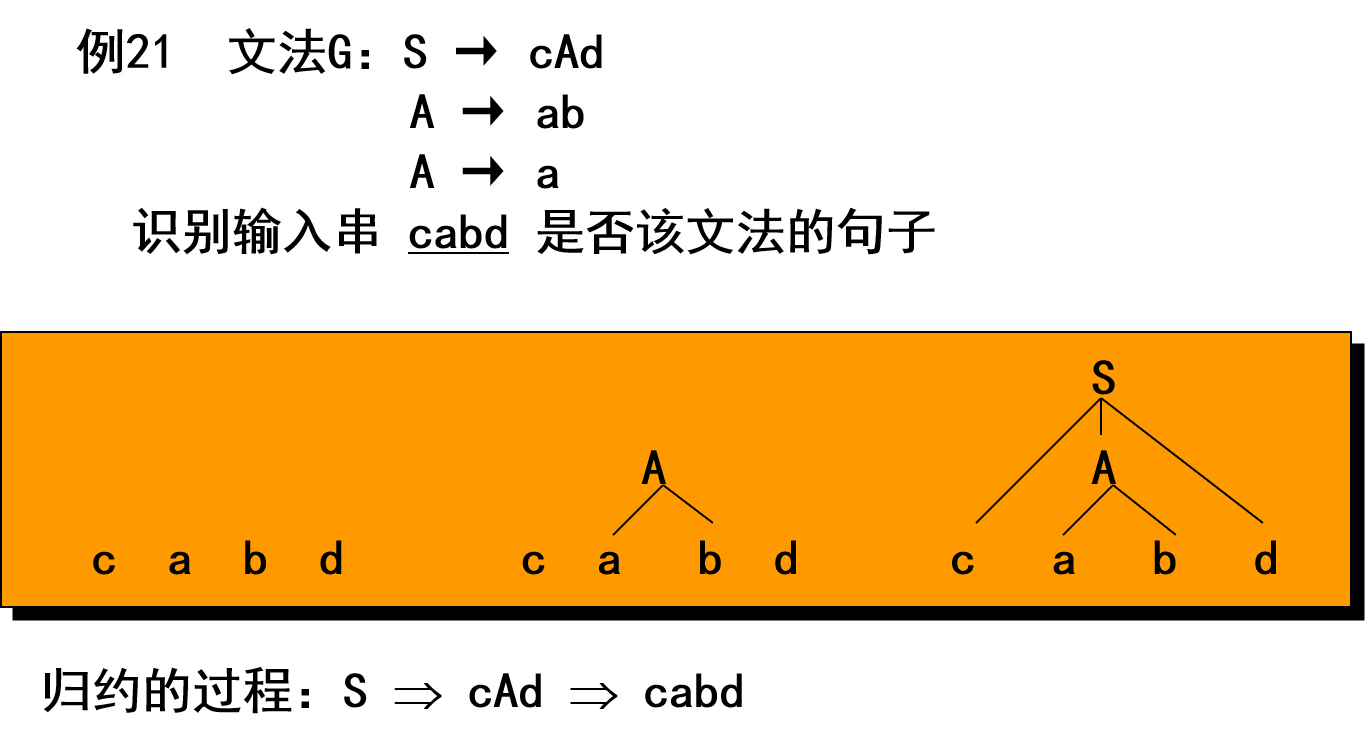
2.6.3 句型分析的有关问题
(1)如何选择使用哪个产生式进行推导?
假定要被代换的最左非终结符号是$V$,且有$n$条规则:$V\rightarrow A_1|A_2|\dots|A_n$,那么如何确定用哪个右部去替代$V$?
(2)如何确定“可归约串”?
在自下而上的分析方法中,在分析程序工作的每一步,都是从当前串中选择一个子串,将它归约到某个非终结符号,该子串称为“可归约串”。如何确定“可归约串”?
以上问题引出以下概念。
短语:文法$G[S],\alpha\beta\delta$是$G$的一个句型,如果$S\Rightarrow^*\alpha A\delta$且$A\Rightarrow^+\beta$,则称$\beta$是句型$\alpha\beta\delta$相对于非终结符$A$的短语。
直接短语:若有$A\Rightarrow\beta$则称$\beta$是句型$\alpha\beta\delta$相对于规则$A\rightarrow\beta$的直接短语(或简单短语)。
句柄:一个句型的最左直接短语称为该句型的句柄。
2.7 有关文法实际应用的一些说明
2.7.1 有关文法的实用限制
实际应用中,需要对文法提出一些限制条件,但这些限制并不真正限制该文法描述的语言。
限制1:文法中不得含有“有害规则”,即引起文法二义性的规则。如$A\rightarrow A$。
限制2:文法中不得含有“多余规则”,即文法中任何句子的推导都用不到的规则,如规则中有不可到达的$V_N$或不可终止的$V_N$。为保证无多余规则,必须满足:1)$A$必须在某句型中出现。2)必须能从$A$推出终结符号串$t$来。
限制3:不含“左递归”规则,如$A\rightarrow A\dots$。
限制4:不含“空规则”,如$A\rightarrow\epsilon$。
2.7.2 上下文无关文法中的$\epsilon$规则
定理2.1 若$L$是由文法$G=(V_N,V_T,P,S)$产生的语言,$P$中的每一个产生式的形式均为$A\rightarrow\alpha$,其中$A\in V_N,\alpha\in(V_N\cup V_T)^*$(即$\alpha$可能为$\epsilon$),则$L$能由这样的一种文法产生,即每一个产生式或者为$A\rightarrow\beta$形式,其中$A$为一个非终结符,即$A\in V_N,\beta\in(V_N\cup V_T)^+$;或者为$S\rightarrow\epsilon$形式,且$S$不出现在任何产生式的右边。
定理2.2 如果$G=(V_N,V_T,P,S)$是一个上下文有关文法,则存在另一个上下文有关文法$G1$,它所产生的语言与$G$产生的相同,其中$G1$的开始符号不出现在$G1$的任何产生式的右边。又如果$G$是一个上下文无关文法,也能找到这样一个上下文无关文法$G1$;如果$G$是一个正规文法,则也能找到这样一个正规文法$G1$。