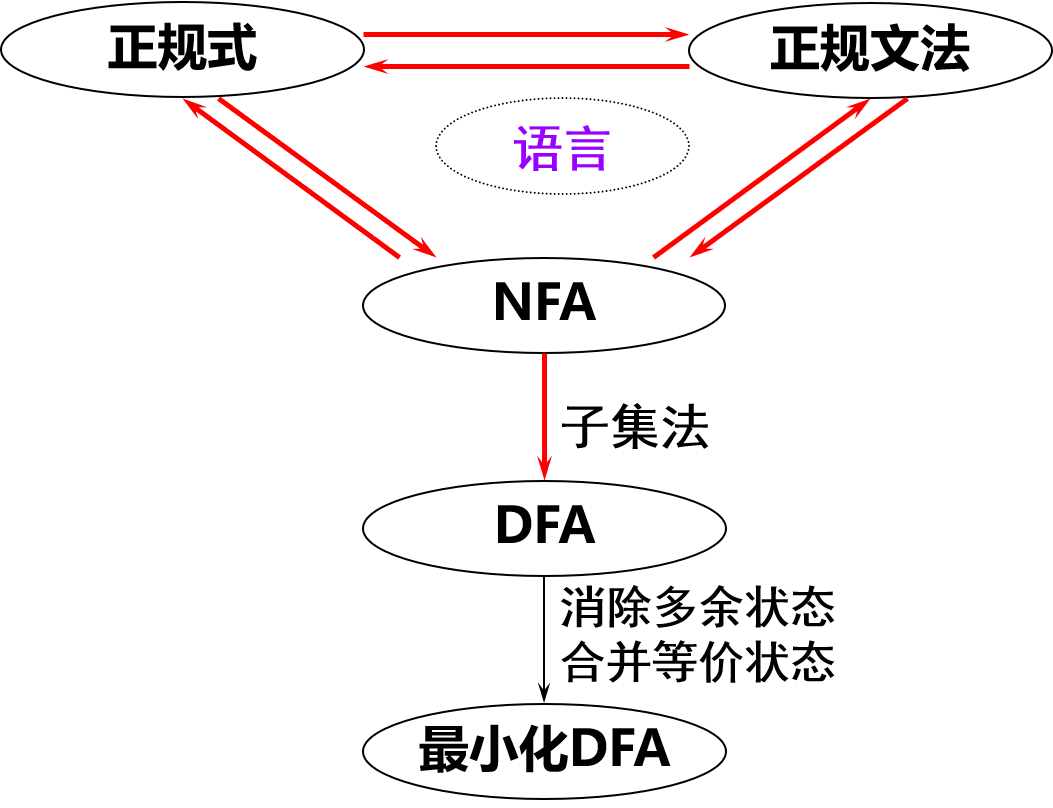
3.1 词法分析程序的设计
词法分析(lexical analysis)功能:逐个读入源程序字符,输出“单词符号”,供语法分析使用。还有滤掉空格,跳过注释、换行符,追踪换行标志,复制出错源程序,宏展开等功能。
3.1.1 词法分析程序和语法分析程序的接口方式
方式一(常用):词法分析程序扫描整个待编译的程序,输出中间文件二元式(单词种类,值),作为语法分析程序的输入。优点是整个编译结构简洁、清晰、条理化,可移植性好。
方式二:语法分析程序调用词法分析程序,返回一个单词。
3.1.2 词法分析程序的输出
在识别出单词同时验证其词法正确性后,词法分析程序将结果以单词符号的形式发送至语法分析程序以回应其请求。单词符号一般分为以下5类。
基本字(关键字):begin, end, if, while
标识符:各种名称,如常量名、变量名、过程名
常数(量):25, 3.1415, TRUE, “ABC”等
运算符:如 + - * / < <=等
界符:逗号,分号,括号等
词法分析程序所输出的单词符号可以采用以下二元式表示:(单词种别,单词自身的值)
3.1.3 将词法分析工作分离的考虑
把编译过程的分析工作划分成词法分析和语法分析两个阶段,主要考虑因素如下:使整个编译程序的结构更简洁、清晰和条理化;编译程序的效率会改进;增强编译程序的可移植性。
3.1.4 词法分析程序中如何识别单词
描述一个语言的词法规则,通常需要借助形式化或半形式化的描述工具。常见的用于词法规则描述的工具有状态转换图、扩展巴克斯范式(EBNF)、有限状态自动机、正规表达式以及正规文法等。
3.2 单词的形式化描述工具
3.2.1 正规文法
正规文法也称正则文法,3型文法。
文法的每个产生式的形式都为:
A$\rightarrow aB$或$A\rightarrow a$(右线性)
$A\rightarrow Ba$或$A\rightarrow a$(左线性)
其中$A,B\in V_N,a\in V_T^*$。例如
标识符的正规文法:(若$i$表示任一字母,$d$表示任一数字)
<标识符>$\rightarrow i|i$<字母数字>
<字母数字>$\rightarrow i|d|i$<字母数字>$|d$<字母数字>
无符号整数的正规文法:<无符号整数>$\rightarrow d|d$<无符号整数>
运算符的正规文法:
<运算符>$\rightarrow +|-|*|/|=|<$<等号>$| >$<等号>$\dots \dots$
<等号>$\rightarrow =$
界符的正规文法:<界符>$\rightarrow , | ; | ( | ) |\dots\dots$
3.2.2 正规式
正规式(regular expression)也称正则表达式,是描述单词符号串的工具。
设字母表$\Sigma={a,\dots,z,A,\dots,Z,0,\dots,9}$
辅助字母表$\Sigma’={\empty,\epsilon,|,\cdot,*,(,)}$
”$*$“表示”闭包”,即任意有限次的自重复连接
“$\cdot$”表示“连接”,有时可以省略
“|”表示“或”
优先顺序为“()”、“*”、“$\cdot$”、“|”
“*”、“$\cdot$”和“|”都是左结合的
正规式为$\empty,\epsilon,\Sigma,(e),e_1|e_2,e_1\cdot e_2,e^*$中的符号,其中$e$表示任一正规式。
若两个正规式$e_1$和$e_2$所表示的正规集相同,则说$e_1$和$e_2$等价,记作$e_1=e_2$。
设$r,s,t$为正规式,则有:
$r|s=s|r$“或”的交换律
$r|(s|t)=(r|s)|t$“或”的可结合律
$(rs)t=r(st)$“连接”的可结合律
$r(s|t)=rs|rt,(s|t)r=sr|tr$分配律
$\epsilon r=r,r\epsilon=r$ $\epsilon$是“连接”的恒等元素
$r|r=r$“或“的抽取律
程序中的单词符号都能用正规式表示$e=<字母>(<字母>|<数字>)^*$
3.2.3 正规文法和正规式的等价性
一个正规语言可以有正规文法定义,也可以由正规式定义。
1.将正规式转换成正规文法
将$\Sigma$上的一个正规式$r$转换成文法$G=(V_N,V_T,S,P)$。令$V_T=\Sigma$,确定产生式和$V_N$的元素用如下办法:
选择一个非终结符$S$生成类似产生式的形式:$S\rightarrow r$,并将$S$定为$G$的识别符号。为表述方便,将$S\rightarrow r$称作正规式产生式,因为在$\rightarrow$的右部中含有“.”、“*”或“|”等正规式符号,不是$V$中的符号。
若$x$和$y$都是正规式,对形如$A\rightarrow xy$的正规式产生式,重写成$A\rightarrow xB,B\rightarrow y$两个产生式,其中$B$是新选择的非终结符,即$B\in V_N$。
对形如$A\rightarrow x^*y$的正规式产生式,重写为
$A\rightarrow xB$
$A\rightarrow y$
$B\rightarrow xB$
$B\rightarrow y$
其中$B$为一个新的非终结符。
对形如$A\rightarrow x|y$的正规式产生式,重写为
$A\rightarrow x$
$A\rightarrow y$
不断利用上述规则做变换,直到每个产生式都符合正规文法的形式。
2.将正规文法转换为正规式
| 文法产生式 | 正规式 | ||
|---|---|---|---|
| 规则1 | $A\rightarrow xB$ $B\rightarrow y$ | $A=xy$ | |
| 规则2 | $A\rightarrow xA | y$ | $A=x^*y$ |
| 规则3 | $A\rightarrow x$ $A\rightarrow y$ | $A=x | y$ |
3.3 有穷自动机
有穷自动机(FA,Finite Automata)是一个识别装置,用于识别“所有句子”,引入目的是为词法分析程序的自动构造寻找特殊的方法和工具。分为确定的和不确定的。
3.3.1 确定的有穷自动机(DFA)
一个确定的有穷自动机$M$是一个五元组
$M=(K,\Sigma,f,S,Z)$
$K$:有穷的状态集
$\Sigma$:有穷的字母表(即输入字符的集合)
$f$:转换函数$K\times\Sigma\rightarrow K$上的映像
$S$:初态(唯一)
$Z$:终态集(不唯一)
DFA的直观表示:
1.状态转换图:每个状态用结点表示;若$f(K_i,a)=K_j$,则$k_i\rightarrow^ak_j$;初态用“$\Rightarrow$” 或 “$-$”标出,终态用双圈或“$+$”标出。
2.矩阵:行表示状态,列表示输入符号,矩阵元素表示相应状态和输入符号将转换成的新状态,可以用“$\Rightarrow$”标明初态,否则第一行即是初态,相应终态行在表的右端标以1,非终态标以0。
若$t\in\Sigma^*$,且存在$f(S,t)=\dots=P,P\in$终态集,则$t$为该DFA可以接受的句子。即:从初态$S$到某终态结点$P$的道路上,所有弧上的标记符连接而成字符串$t$,$t$为该DFA可以接受的句子。DFA $M$能够接受的句子的全体记为$L(M)$。
$f:K\times\Sigma\rightarrow K$是一个单值函数,即对任何状态$K$,当输入字符$a$时,下一状态唯一。
3.3.2 不确定的有穷自动机(NFA)
一个不确定的有穷自动机$M$是一个五元组
$M=(K,\Sigma,f,S,Z)$
$K$:有穷的状态集
$\Sigma$:有穷的字母表(即输入字符的集合)
$f$:转换函数$K\times\Sigma^*\rightarrow K^+$上的映像($K^+$表示$K$的子集)
$S$:初态(不唯一)
$Z$:终态集(不唯一)
NFA的直观表示:
1.状态转换图:每个状态用结点表示;若$f(K_i,a)=K_j$,则$k_i\rightarrow^ak_j$;初态用“$\Rightarrow$” 或 “$-$”标出,终态用双圈或“$+$”标出。
2.矩阵:行表示状态,列表示输入符号,矩阵元素表示相应状态和输入符号将转换成的新状态,可以用“$\Rightarrow$”标明初态,否则第一行即是初态,相应终态行在表的右端标以1,非终态标以0。
若$t\in\Sigma^*$,且存在$f(S,t)=\dots=P,P\in$终态集,则$t$为该DFA可以接受的句子。即:从初态$S$到某终态结点$P$的道路上,所有弧上的标记符连接而成字符串$t$,$t$为该NFA可以接受的句子。NFA $M’$能够接受的句子的全体记为$L(M’)$。对于每个NFA $M’$,存在一个DFA $M$,使得$L(M’)=L(M)$。
$\epsilon$可以被NFA $M’$接受的两种情况:$M’$的某结点既是初态,又是终态;存在一条从初态到终态的$\epsilon$道路。
对于状态$K$,当输入字符$a$时,下一状态不一定唯一。
对每个NFA $M’$,一定存在一个DFA $M$,使得$L(M’)=L(M)$,即:对每个NFA $M$,存在着与之等价的DFA $M’$。与某一NFA等价的DFA不唯一。
3.3.3 NFA转换为等价的DFA
1.基本运算
状态集合$I$的$\epsilon$闭包:表示为$\epsilon-closure(I)$。状态集$I$中的任何状态$S$经任意条$\epsilon$弧而能到达的状态的集合。状态集$I$的任何状态$S$都属于$\epsilon-closure(I)$。
状态集合$I$的$a$弧转换:表示为$mova(I,a)$。定义为状态集合$J$,其中$J$是所有那些可从$I$的某一状态经过一条$a$弧而到达的状态的全体。
2.转换的主要思想
DFA的一个状态可能对应NFA的一个或一组状态。
DFA同样记录在NFA上读入某个$V_T$后可能到达的所有状态。
3.子集法
NFA $N=(K,\Sigma,f,K_0,K_t)$构造DFA $M=(S,\Sigma,d,S_0,S_t)$,使得$L(M)=L(N)$:
(1)$M$的状态集$S$由$K$的一些子集组成
(2)$M$和$N$的输入字母表相同
(3)转换函数$d$是这样定义的:$d([S_1,\dots,S_j],a)=\epsilon-closure(move([S_1,\dots,S_j],a))$
(4)$S_0=\epsilon-closure(K_0)$为$M$的开始状态
(5)$S_t={[S_i,S_k,\dots,S_e]$,其中$[S_i,S_k,\dots,S_e]\in S$且${S_i,S_k,\dots,S_e}\cap K_t\neq\empty}$。
构造NFA $N$的状态$K$的子集的算法:
假定所构造的子集族为$C=(T_1,T_2,\dots,T_i)$,其中$T_1,T_2,\dots,T_i$为状态的子集。
a. 开始,令$\epsilon-closure(K_0)$为$C$中唯一成员,并且它是未被标记的。
b. While(C中存在尚未被标记的子集T) do
{ 标记T;
for(每个输入字母a) do
{ U:= $\epsilon$-closure(move(T,a));
if(U不在C中) then
{ 将U作为未标记的子集加在C中;}
}
}
3.3.4 确定有穷自动机的化简
DFA的化简也称最小化DFA,指没有多余状态,没有两个状态是互相等价的DFA。
多余状态:从开始状态出发,任何输入串也不能到达的状态。处理:消除多余状态
两个状态s和t等价,满足:一致性,同是终态或同时非终态;蔓延性,从s出发读入某个$a(a\in\Sigma)$和从t出发读入某个a到达的状态等价。处理:合并等价状态(使用“分割法”)
3.4 正规式和有穷自动机的等价性
对于$\Sigma$上的NFA M,可以构造一个$\Sigma$上的正规式$R$,使得$L(R)=L(M)$。
对于$\Sigma$上的正规式$R$,可以构造一个$\Sigma$上的NFA M,使得$L(M)=L(R)$。
$FA\rightarrow$正规式:在FA M的状态图上加两个状态结点x和y,从x结点出发,用$\epsilon$弧连接x结点到所有初态结点,从M的所有终态结点用$\epsilon$弧连接到y结点,此时x为初态,y为终态。利用消结规则,逐步消去M’中的所有结点,直至只剩下x和y,最后x和y结点间的弧上的标记则为所求的正规式R。
正规式$\rightarrow FA$:将正规式分解成一系列子表达式,对于每个子表达式,用如下规则构造FA。
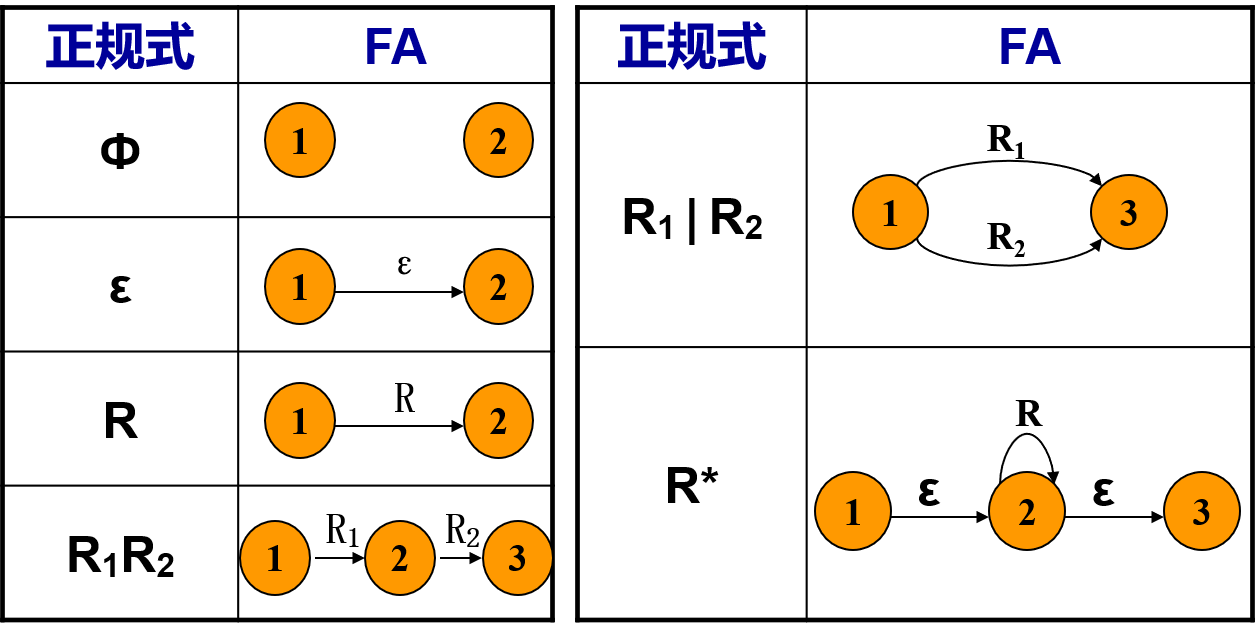
3.5 正规文法和有穷自动机的等价性
正规文法$\rightarrow FA$:输入字符集与正规文法的$V_T$相同,状态集与正规文法中的$V_N$相同。左线性正规文法的转换规则:增加一个初态结点,开始符号对应的结点作为终态;对形如$A\rightarrow t$的规则,引一条从初始状态到$A$的弧,标记为$t$;对形如$A\rightarrow Bt$的规则,引一条从$B$到$A$的弧,标记为$t$。右线性正规文法的转换规则:增加一个终态结点,开始符号对应的结点作为初态;对形如$A\rightarrow t$的规则,引一条从$A$到终态结点的弧,标记为$t$;对形如$A\rightarrow tB$的规则,引一条从$A$到$B$的弧,标记为$t$。($t$为$V_T$或$\epsilon$)。
$FA\rightarrow$正规文法:与$f(A,a)=B$对应的产生式为$A\rightarrow aB$,对终态结点$Z$,增加产生式$Z\rightarrow\epsilon$,NFA的初态对应文法的开始符号,NFA的输入字符集对应文法的$V_T$。