网络层与运输层的不同之处在于，运输层只存在于主机中，为不同主机进程之间提供通信服务，而网络层存在于主机和路由器中，为不同主机之间提供通信服务。

3.1　运输层提供的服务

运输层为不同主机进程间提供端到端的逻辑通信功能(无需考虑具体物理链路)。

运输层协议运行在端系统，不在路由器中。发送方运输层将应用进程的报文划分成若干报文段，封装后传给网络层；接收方运输层将网络层上传的报文段，去掉运输层首部后，重新装配为报文，传向应用层。双方网络层负责主机到主机的网络传输，提供主机之间的逻辑通信。

运输层协议有TCP和UDP，提供不同的服务质量，所能提供的服务受到网络层提供服务的限制，如不保证时延和带宽。同样，网络层服务是不可靠的(存在分组丢失、失序和重复)，运输层协议通过检错重传、排序、查重等措施能为应用程序提供可靠的传输服务。

网络层的主要协议是IP(网际协议)，TCP和UDP都基于IP。IP提供不可靠的传输服务，尽最大的努力在通信的主机之间交付数据报，但不保证按序交付和数据的完整性。IP使用IP地址，即设备接口的网络层地址，每台主机至少有一个，路由器有多个。

应用层的作用是为用户的分布式应用程序提供访问网络的接口。

2.1　应用层的基本概念

2.1.1　网络应用程序的体系结构

网络应用程序的体系结构指在各端系统上的分布式应用程序的工作模式，由研发者决定，分为客户机/服务器模式(C/S)和对等模式(P2P)。

客户机/服务器模式：服务器通常一直运行，具有固定的IP地址，可为多个客户机提供服务，可扩展为服务器集群。客户机偶尔开机，具有固定或动态的IP地址，向服务器发出请求，客户机之间不直接通信。大部分网络应用如Web应用、电子邮件、文件传输采用该模式。

P2P模式：无(或很少使用)服务器。如果有服务器，也只用于如注册IP地址、登记用户、计费等。端系统(对等方)之间直接数据通信，既请求服务，也提供服务。对等方IP地址可以不固定。BT、QQ、Skype等采用该模式。

计算机网络从20世纪60年代发展至今，是计算机技术与通信技术相结合的产物，其定义如下

定义　计算机网络是用通信设备和通信链路连接起来，使用网络协议进行数据通信，实现资源共享的计算机的集合。

计算机网络由硬件和软件组成，硬件为

通信子网：通信设备和通信介质，用来传输数据；

资源子网：计算机及其硬件，用来存储和处理数据。

软件为

一系列网络协议：保证数据通信正确进行。

计算机网络类型众多，如局域网、广域网；有线网、无线网。最大的计算机网络为因特网。

Description

恰逢H国国庆，国王邀请n位大臣来玩一个有奖游戏。首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。然后，让这n位大臣排成一排，国王站在队伍的最前面。排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是：排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。注意，国王的位置始终在队伍的最前面。

Input

第一行包含一个整数n，表示大臣的人数。

第二行包含两个整数a和b，之间用一个空格隔开，分别表示国王左手和右手上的整数。

接下来n行，每行包含两个整数a和b，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。

Output

一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。

Sample Input

1
2
3
4
5

3 
1 1 
2 3 
7 4 
4 6

Sample Output

1

2

k近邻法(k-NN)|第11天

Steps

Datasets

第5章　神经网络

5.1　神经元模型

神经网络(neural networks)是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

神经网络中最基本的成分是神经元(neuron)模型。如果某神经元的电位超过了一个”阈值”(threshold)，那么它就会被激活。上述情形可以抽象为图5.1所示的简单模型，即”M-P神经元模型”。在这个模型中，神经元接收到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接(connection)进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过”激活函数”(activation function)处理以产生神经元的输出。

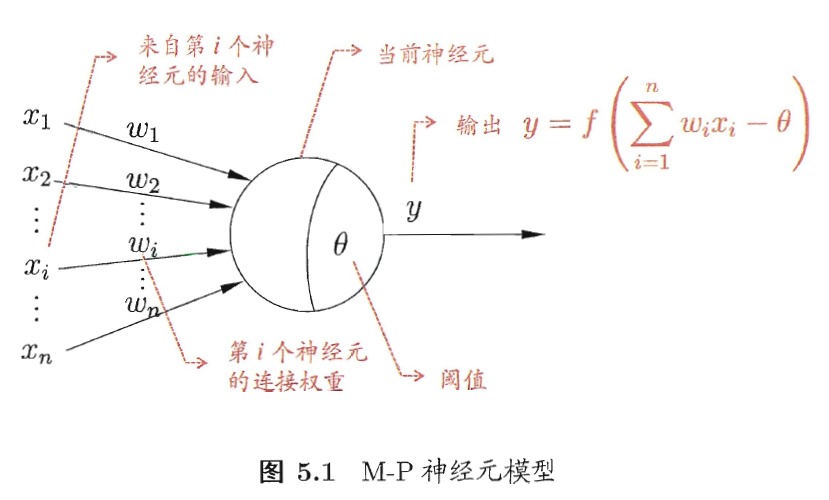
理想的激活函数是图5.2(a)所示的阶跃函数，将输入值映射为输出值”0”(神经元抑制)或”1”(神经元兴奋)。然而碍于其性质，实际常用如图5.2(b)的Sigmoid函数作为激活函数也称为”挤压函数”(squashing function)。

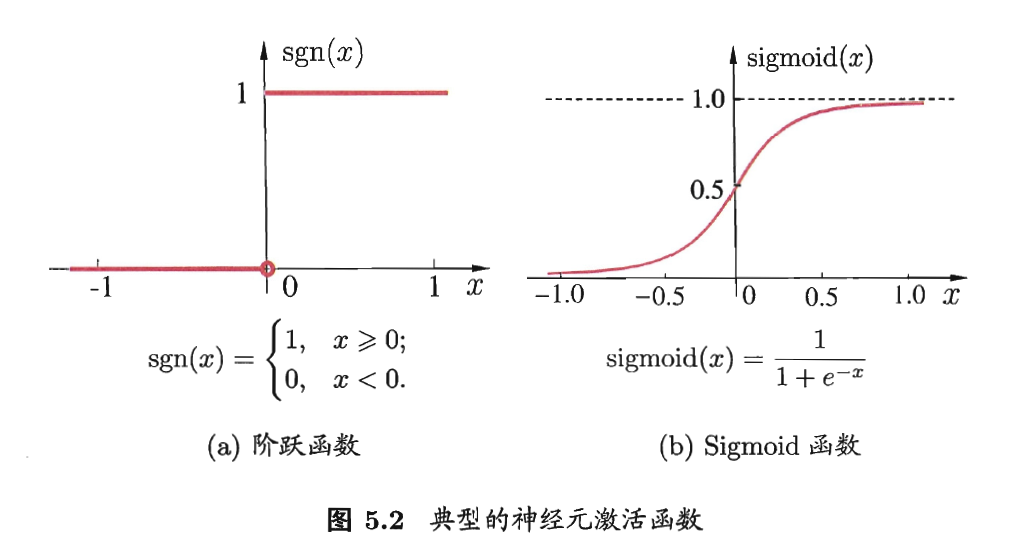
事实上，可以将一个神经网络视为包含了许多参数的数学模型，这个模型是若干个函数，例如$y_i=f(\sum_iw_ix_i-\theta_j)$相互(嵌套)代入而得。

Description

The French author Georges Perec (1936–1982) once wrote a book, La disparition, without the letter ‘e’. He was a member of the Oulipo group. A quote from the book:

Tout avait Pair normal, mais tout s’affirmait faux. Tout avait Fair normal, d’abord, puis surgissait l’inhumain, l’affolant. Il aurait voulu savoir où s’articulait l’association qui l’unissait au roman : stir son tapis, assaillant à tout instant son imagination, l’intuition d’un tabou, la vision d’un mal obscur, d’un quoi vacant, d’un non-dit : la vision, l’avision d’un oubli commandant tout, où s’abolissait la raison : tout avait l’air normal mais…

Perec would probably have scored high (or rather, low) in the following contest. People are asked to write a perhaps even meaningful text on some subject with as few occurrences of a given “word” as possible. Our task is to provide the jury with a program that counts these occurrences, in order to obtain a ranking of the competitors. These competitors often write very long texts with nonsense meaning; a sequence of 500,000 consecutive ‘T’ s is not unusual. And they never use spaces.So we want to quickly find out how often a word, i.e., a given string, occurs in a text. More formally: given the alphabet {‘A’, ‘B’, ‘C’, …, ‘Z’} and two finite strings over that alphabet, a word W and a text T, count the number of occurrences of W in T. All the consecutive characters of W must exactly match consecutive characters of T. Occurrences may overlap.

Input

The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:

• One line with the word W, a string over {'A', 'B', 'C', …, 'Z'}, with 1 ≤ |W| ≤ 10,000 (here |W| denotes the length of the string W).
• One line with the text T, a string over {'A', 'B', 'C', …, 'Z'}, with |W| ≤ |T| ≤ 1,000,000.

Output

For every test case in the input file, the output should contain a single number, on a single line: the number of occurrences of the word W in the text T.

Sample Input

1
2
3
4
5
6
7

3
BAPC
BAPC
AZA
AZAZAZA
VERDI
AVERDXIVYERDIAN

Sample Output

1
2
3

1
3
0

第4章　决策树

4.1　基本流程

决策树(decision tree)是基于树结构进行决策的一种常见机器学习方法。

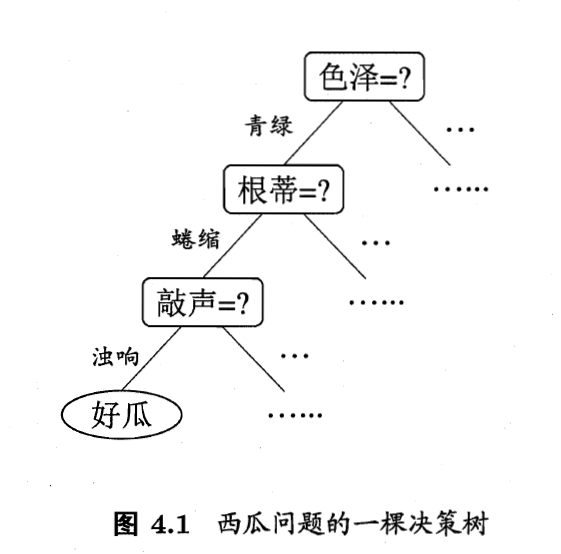
决策过程的最终结论对应了所希望的判定结果；决策过程中提出的每个判定问题都是对某个属性的”测试”；每个测试或是导出结论，或是导出进一步的判定问题，其考虑范围是在上次决策结果的限定范围之内。

一般的，一棵决策树包含一个根结点、若干个内部结点和若干个叶节点；叶结点对应于决策结果，其他每个结点对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集。从根结点到每个叶结点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一棵泛化能力强的决策树，基本流程遵循”分治”(divide-and-conquer)策略。

逻辑回归|第6天

Steps

Datasets

数据集包含了社交网络中用户的信息。这些信息涉及用户ID,性别,年龄以及预估薪资。一家汽车公司刚刚推出了他们新型的豪华SUV，尝试预测哪些用户会购买这种全新SUV。并且在最后一列用来表示用户是否购买。将建立一种模型来预测用户是否购买这种SUV，该模型基于两个变量，分别是年龄和预计薪资。因此特征矩阵将是这两列。我们尝试寻找用户年龄与预估薪资之间的某种相关性，以及他是否购买SUV的决定。